
1 アルゴリズムの説明
1.1 基礎式
非定常三次元非圧縮性粘性流れの熱移動を考慮した基礎式は、
次式のような無次元化したNavier-Stokes方程式と連続の式により表される。
![]() (1)
(1)
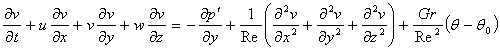 (2)
(2)
![]() (3)
(3)
![]() (4)
(4)
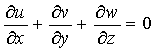 (5)
(5)
ただし、 p:圧力(=p/ρ) u, v, w:x方向,y方向,z方向の速度
θ:温度 θ0:周囲温度 t:時間 Re:レイノルズ数
Pr:プラントル数 Gr:グラスホフ数 Ra:レーリー数 である。
境界条件はu,v,wについて、 ![]() または
または ![]()
![]() または
または ![]()
![]() または
または ![]()
![]() または
または ![]() とする。
とする。
1.2 有限要素法による定式化(MSR解法)(1)
(1)解法の方針
圧力、速度についてはSIMPLER法と同様の考え方で解く。
また式(1)〜式(4)を移流拡散方程式とみなし、変形ガレルキン法により定式化する。
この解法をMSR解法とよぶ。MSR解法ではΔt時間前の速度uから
圧力pの予測値p*を求める。
(2)圧力予測値の導出
式(1)の非定常項を![]() 、圧力p'をpm+1の予測値p*と考え、
、圧力p'をpm+1の予測値p*と考え、
式(1)を二段階に分けて考えると次式のように表わされる。
第一段階
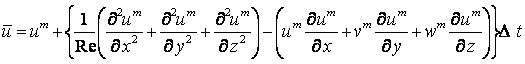 (6)
(6)
第二段階
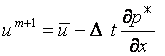 (7)
(7)
式(2)、式(3)も同様に考えると次式を得る。
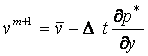 (8)
(8)
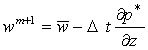 (9)
(9)
ここで式(6)と式(7)の和は式(1)になる。式(6)より疑似速度![]() が求まる。
が求まる。
また式(7)をx、式(8)をy、式(9)をzで偏微分し、これらを足しあわせ
連続の式(5)を考慮するとp*に関する関するポアソン方程式が得られる。
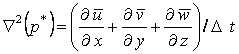 (10)
(10)
ガレルキン法により定式化すると次式のような連立方程式が得られる。
![]()
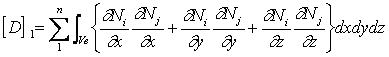
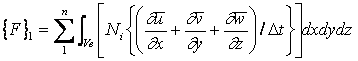
これにより圧力の予測値p*が求まる。
(3)各運動方程式の変形ガレルキン法による定式化
上記で求めた圧力の予測値を![]() として考えると、
として考えると、
非線形方程式の式(1)は次式のように表される。
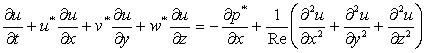 (11)
(11)
u*,v*,w* をΔt 時間前の値により近似すると、上式は線形方程式と
考えることができる。よって式(11)は移流拡散方程式と見なすことができ、
この式を変形ガレルキン法により定式化することによりu,v,w が得られる。
すなわち、次式を得る。
![]() (12)
(12)
いま φをタイム・スキーム・パラメータとし、(1-φ)×式(12)t-Δt+ φ×式(12)t を
つくり、式(13)を利用して変形すると式(14)を得る。
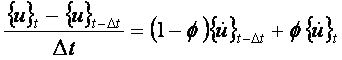 (13)
(13)
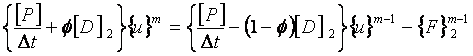 (14)
(14)

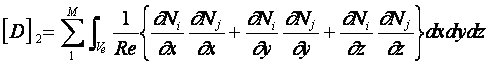
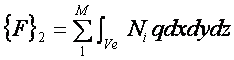
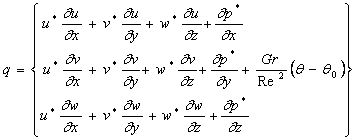
ただし,Δt :タイム・ステップ n :時間方向の添字 Ve :一要素の領域
M :総要素数 N :形状関数 φ :タイム・スキーム・パラメータ である。
(4)δp の導出につぃて
予測値![]() から求められた流速値
から求められた流速値![]() は近似値であるため、これらを
は近似値であるため、これらを![]() とする。
とする。
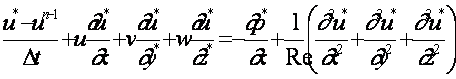 (15)
(15)
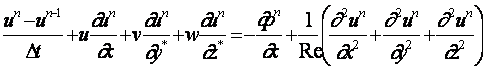 (16)
(16)
したがって両式の差をとって![]() とおくことにより次式が得られる。
とおくことにより次式が得られる。
ただし各省略項(移流項,粘性項,浮力項)は補正量に関係したものなので
無視している。
![]() (17)
(17)
同様に下記の式が得られる。
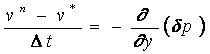 (18)
(18) ![]() (19)
(19)
式(17)をx、式(18)をy、式(19)をzにより偏微分し、これらを足し
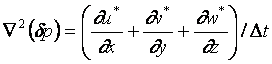 (20)
(20)
上式をガレルキン法により定式化すると次式のような連立方程式が得られる。
![]() (21)
(21)
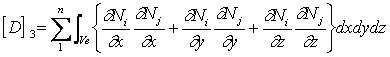
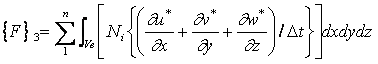
(5)各流速および圧力の導出
式(21)を解いて![]() が求まり、結局次式より
が求まり、結局次式より![]() を得ることができる。
を得ることができる。
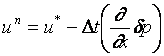
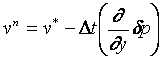
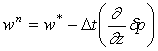
![]()
(6)形状関数と移流項の評価方法
u,v,w及びpいずれも形状関数として六面体一次要素を考える。
移流項の評価方法としては、次式のように速度は要素ごとにCの
一階微分項は各節点ごとに振り分けて評価する。
 (22)
(22)
1.3 補正係数の導入
拡散項にf、移流項にgの補正係数を導入するが、
下図のような六面体1次要素での補正係数をいかに示す。(3)
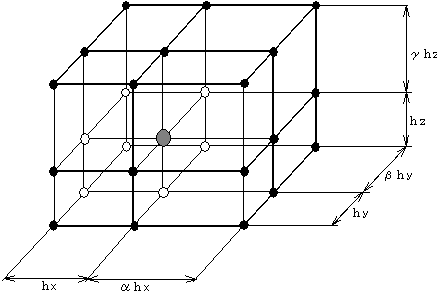
図1.1 不等長六面体一次要素
(1)不等長要素の場合
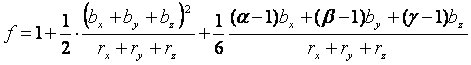 (23)
(23)
![]()
(2)等長要素の場合
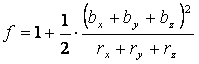 (24)
(24)
![]()
以 上