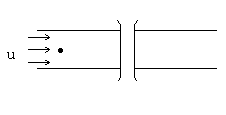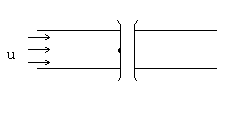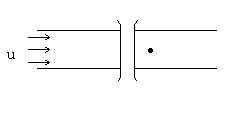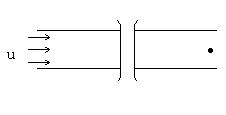
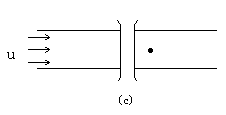
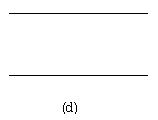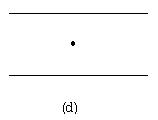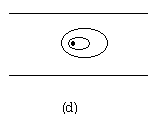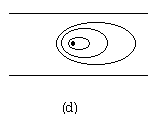
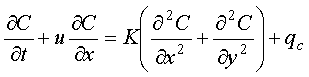| 戻る 3.4 重要なのは移流拡散方程式 いま図6のような2次元x−y空間座標において、 流速uで流れている川にかかった橋の上からインクを瞬間的に 落としたとしましょう。(図6(a)) この際、インク自体は川の中で”じわっと拡がる”でしょうし (図6(b))、また川の流れによっても運ばれることになります。 (図6(c)) したがって最終的なインク濃度の拡がりの分布は図6(d)の ような濃度の等高線で表されるでしょう。 この場合インクの 濃度をCとすると、その拡がりについてのモデル式は、 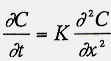 のy方向への拡散を考慮した式と のy方向への拡散を考慮した式と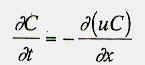 とから、 とから、次式により表されます。
|
|||||||||