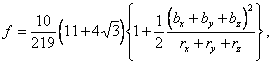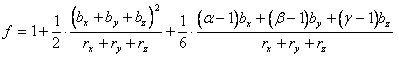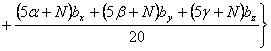変形ガレルキン法における補正係数の導出方法については一次元移流拡散問題の
等長要素と不等長要素について述べてきたが、この技法は二次元及び三次元問題についても
理論的に拡張できる.その詳細については関連文献(15〜20)を参照して頂くとして、
本章ではその結果を中心にまとめた.
8.1 二次元移流拡散方程式の定式化
本節では変形ガレルキン法の二次元移流拡散問題への適用について簡単に述べ、各種二次元
分割形状要素についての補正係数を紹介する。二次元非定常移流拡散方程式についても、一次元問題と
同様に移流項を発生項とみなして陽的に離散化すると対称マトリックスのみによる連立方程式を得る。
同時に精度の向上と安定性の改善のため、拡散項に補正係数![]() を移流項に補正係数
を移流項に補正係数![]() を導入する。
を導入する。
これらの補正係数は二次元移流拡散方程式の一般解の増幅因子と移流項を陽的に定式化
した数値解での増幅因子とを等値することにより求められる。そして![]() 方向の波数
方向の波数![]() と
と![]() 方向の波数
方向の波数![]() に
に
依らない補正係数を得るために![]() と
と![]() の極限を考えると、変形ガレルキン法における各種
の極限を考えると、変形ガレルキン法における各種
三角形要素、四辺形要素および混合要素についての補正係数が得られる。また理論誤差および
数値計算誤差での他の有限要素解法および差分解法との比較により、変形ガレルキン法は
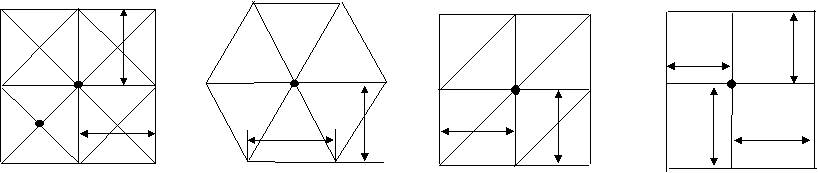
高精度となることが示されている(15〜18)。 たとえば図6-1のような各種形状要素に囲まれた
各節点での変形ガレルキン法による補正係数を次式にまとめて示す。
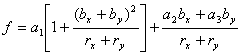 ,
, ![]() (6-1)
(6-1)
ここで、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() :y方向の流速、
:y方向の流速、
![]() と
と![]() :xとy方向の拡散係数、
:xとy方向の拡散係数、![]() と
と![]() :xとy方向のメッシュ幅の変化率、TE及びTESは直角
:xとy方向のメッシュ幅の変化率、TE及びTESは直角
三角形要素の組み合わせであり、TRは正三角形要素、RLは長方形要素を示している。
また式(6-1)での各係数![]() 、
、![]() 及び
及び![]() を表6-1に示す.節点RLでの補正係数は一次元
を表6-1に示す.節点RLでの補正係数は一次元
不等長要素補正係数(式(5-21))と同様の形になり、その第3項はメッシュ幅の変化による
打ち切り誤差への修正である。なお任意形状要素での変形ガレルキン法による補正方式
では各補正係数は結局、数値計算により求められるが、本稿では省略した。
Table 6.1 Correction coefficients
|
Node |
|
|
|
|
TE( |
|
0 |
0 |
|
TE( |
|
0 |
0 |
|
TR |
|
|
|
|
TES |
|
|
|
|
RL |
1 |
|
|